ارتفاع المعين
ما أبرز خصائص المعين؟
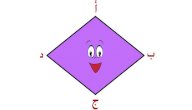
المعين (بالإنجليزية: Rhombus) هو شكلٌ رباعيٌّ مسطّح تتساوى فيه أطوال جميع أضلاعه، وأيضًا تتساوى فيه جميع قياسات زواياه الداخليّة، ومن خصائص المعين أن كلّ ضلعين متقابِلَيْن فيهِ متوازيين، وأيضًا من خصائصه أن أقطاره تتقاطع في زاوية قائمةٍ (أي بقياس 90 درجة) وينصّف كل قطرٍ منهما الآخر، أما ارتفاع المعين (بالإنجليزية: Altitude) فهو المسافة العموديّة بين أيّ ضلعينِ متقابِلَين من أضلاع المعين، [١] ويمكن حساب ارتفاع المعين من خلال القانون الخاص به وهو: ارتفاع المعين = مساحة المعين ÷ طول ضلع المعين، وفي حال عدم توفر مساحة المعين ضمن المعطيات بشكلٍ مباشرٍ، أو عدم توافر طول ضلع المعين، فإنه يمكن استخدام قوانين المعين المختلفة مثل قانون محيط المعين أو قانون مساحة المعين من أجل إيجاد مساحة المعين أو طول الضلع بناء على المجهول منهما ثم استخدام هذه النتائج في قانون ارتفاع المعين. [٢]
مسائل رياضية تطبيقية على حساب ارتفاع المعين
كيف يمكن حساب ارتفاع المعين؟
المعين عبارة عن متوازي أضلاع بأربعة أضلاع متساوية في الطول ومتوازية، وكما ذُكر سابقًا فإنه يمكن حساب ارتفاع المعين باستعمال القانون الخاص به، وهو كالآتي:[٢]
ارتفاع المعين = مساحة المعين ÷ طول ضلع المعين
وبالرموز: ع=م÷ل
حيث إنّ:
- ع هي ارتفاع المعين
- م هي مساحة المعين
- ل هو طول ضلع المعين
ولفهم القانون بشكل أفضل وزيادة مهارة الحصول على ارتفاع المعين بناء على المعطيات المطلوبة في المسائل لا بد من بعض الأمثلة التطبيقية التي تشرح طريقة حساب ارتفاع المعين بشكل أفضل، وهذه بعضها:
- إذا كانت مساحة المعين 64 سم مربّع، وطول ضلعه 8 سم، فما هو ارتفاعه؟
الحل:
باستخدام قانون ارتفاع المعين:
ارتفاع المعين = مساحة المعين ÷ طول ضلع المعين
تصبح المعادلة على هذا النحو:
ارتفاع المعين = 64 ÷ 8
وبالتالي فإن ارتفاع المعين هو "8" سم. [٢]
- إذا كانت مساحة المعين 315 سم مربّع ومحيطه 180سم، فما هو ارتفاعه؟
الحل:
في هذا المثال لا يتوفّر طول ضلع المعين بشكل مباشر، لذا فإنه يتم استخدام قانون محيط المعين لإيجاد طول الضلع، وقانون محيط المعين على هذا النحو: محيط المعين= 4 * طول الضلع
ومنه فإن:
طول الضلع = محيط المعين ÷ 4
وبذلك تصبخ المعادلة على هذا النحو:
طول الضلع= 180 ÷ 4
وبالتالي فإنّ طول الضلع = "45" سم.
الآن يستخدم قانون ارتفاع المعين بعد توفّر طول الضلع والمساحة، وقانون ارتفاع المعين على هذا النحو:
ارتفاع المعين = مساحة المعين ÷ طول ضلع المعين
لتصبح المعادلة على هذا النحو:
ارتفاع المعين = 315 ÷ 45
وبالتالي فإن ارتفاع المعين= "7" سم. [٣]
- إذا كانت أطوال قطريْ معين هي 4 سم و6 سم وكان طول ضلعه 2 سم، فما هو ارتفاعه؟
الحل:
في هذه الحالة يستخدم قانون مساحة المعين الذي يعتمد على أطوال الأقطار وهو على هذا النحو:
مساحة المعين= (القطر الأول*القطر الثاني) ÷ 2
لتصبح المعادلة على هذا النحو:
مساحة المعين= (4*6) ÷ 2
لينتج أن مساحة المعين= "12" سم مربّع.
والآن بعد توافر مساحة المعين وطول الضلع، يستخدم القانون:
ارتفاع المعين= مساحة المعين ÷ طول ضلع المعين
لتصبح المعادلة على هذا النحو:
ارتفاع المعين= 12 ÷ 2
ليكون الناتج "6" سم وهو يمثّل ارتفاع المعين. [٢]
المراجع[+]
- ↑ "Rhombus", www.mathsisfun.com, Retrieved 2020-07-14. Edited.
- ^ أ ب ت ث "How to Find the Height of a Rhombus", sciencing.com, Retrieved 2020-07-14. Edited.
- ↑ "Ask The Expert", www.topperlearning.com, Retrieved 2020-07-14.